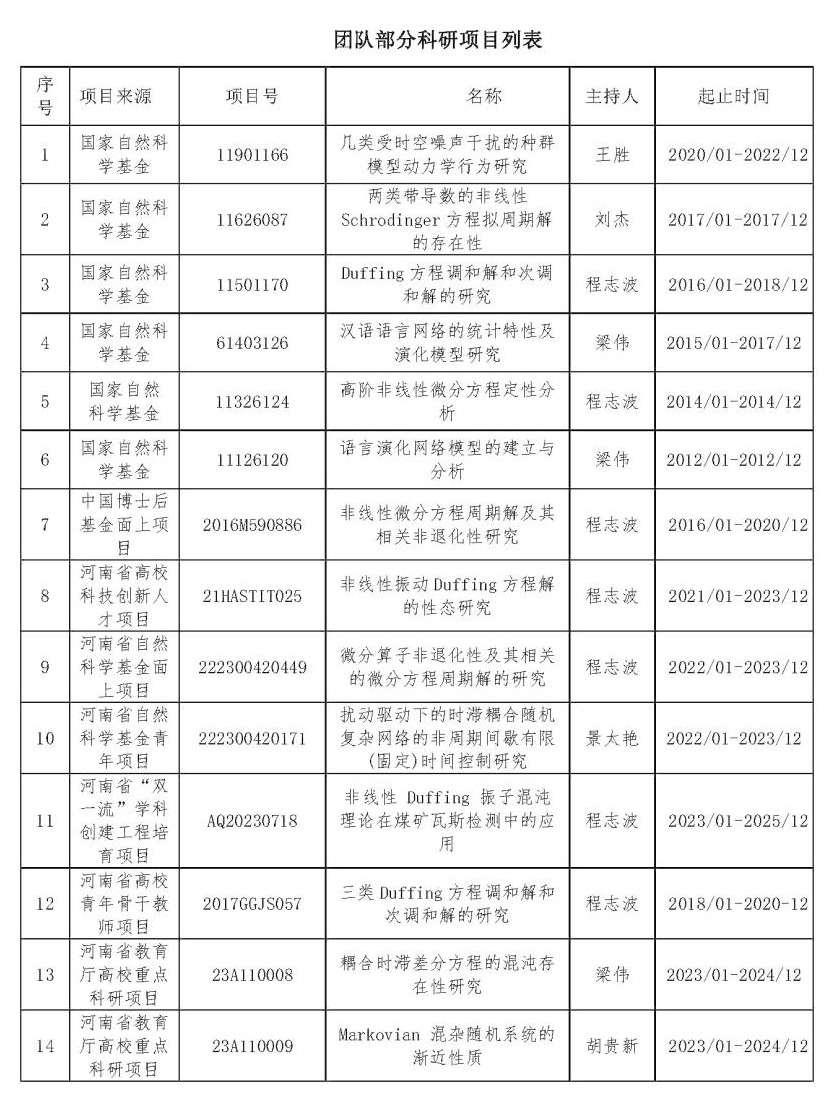
常微分方程与动力系统创新团队的主要研究领域为常微分方程理论及动力系统理论。常微分方程是现代数学的重要组成部分,在众多科学技术领域有着非常广泛的应用。在几何学、力学、天文学、核物理、电子技术、空间技术和星际航空等许多尖端科技领域内,它已成为强有力的杠杆,推动这些学科的发展。在现代的生物学、人工神经网络动力学和经济学等领域,微分方程的理论和方法也是不可缺少的。本团队致力于利用不动点定理和拓扑度理论,研究非线性微分方程(如高阶微分方程、中立型微分方程、奇性微分方程、Duffing方程等)解的存在性(如周期解、周期正解、调和解和次调和解等);利用KAM方法研究有限维和无穷维哈密顿系统的拟周期解和概周期解的存在性;利用分支理论研究反应扩散种群模型的Hopf分支和Turing分支等问题;利用耦合扩张理论和返回扩张不动点理论研究(偏)差分方程的混沌化;利用不动点定理和李雅普诺夫函数研究随机系统的稳定性和随机周期解问题。目前该研究团队在此方面“标志性”成果和创新性贡献简述如下:
(1)利用双算子不动点定理,突破了中立型参数 c 自 1 到无穷时周期解存在性这一研究瓶颈。证明了该方程在中立型参数 c 自负无穷到正无穷时周期解的存在性,在半线性中立型微分方程情形下,把中立型参数 c 的取值范围扩展到最大。
(2)运用耦合扩张理论和返回扩张不动点理论等证明了(偏)差分方程的混沌存在性;将正弦函数和锯齿函数等特殊控制器推广到了一般函数,并且弱化了混沌存在的条件,使受控系统产生混沌变得更加容易、可行,进而为混沌的应用和推广提供了便利。
团队成员介绍
团队现有成员9人,其中博士8人,教授2人,副教授4人,讲师3人,河南省高校科技创新人才1人,河南省教育厅学术技术带头人1人,河南省高校青年骨干教师1人,河南省教学标兵1人,bat365官网登录入口元培学者1人,元培名师3人,校青年骨干教师4人.



代表性论文列表
1. Yongjun Zhang, Wei Liang, Xiaolin Lv, Existence of chaos in controlled first-order partial difference equations with general delay controllers,Chaos, Solitons & Fractals, 168(2023)113148.
2. Cheng Zhibo*, Gu Lulu, Positive periodic solution to a second-order differential equation with attractive-repulsive singularities, Rocky Mountain J. Math. 52 (2022) 77-85.
3. Taiyan Jing,Daoyuan Zhang,Xiaohua Zhang,New criteria for synchronization of multi-layer neural networks via a periodically intermittent control,Computational Intelligence and Neuroscience, (2022),ID 8157794,10 pages.
4. Jiafa Xu, Jie Liu,Donal O’Regan,Infinitely many solutions for a gauged nonlinear Schrodinger equation with a perturbation, Nonlinear Analysis:Modelling and Control , 4(2021), 626-641.
5. Haihong Guo, Wei Liang, Chaotic dynamics of partial difference equations with polynomial maps, International Journal of Bifurcation and Chaos, 31 (2021) 2150133.
6. Weiming Ji , Guixin Hu, Stability and explicit stationary density of a stochastic single-species model, Applied Mathematics and Computation, 390 (2021) 125593.
7. Cheng Zhibo*, Cui Xiaoxiao, Positive periodic solution for generalized Basener-Ross model, Discrete Contin. Dyn. Syst. Ser. B 25 (2020), 4361–4382.
8. Jie Liu, Zhibo Cheng, Yi Wang, Positive periodic solution for second-order nonlinear differential equation with singularity of attractive type, Journal of Applied Analysis and Computation, 4 (2020),1636-1650.
9. Zhan-Ping Ma, Hai-Feng Huo, Hong Xiang, Spatiotemporal patterns induced by delay and cross-fractional diffusion in a predator-prey model describing intraguild predation. Math. Methods Appl. Sci. 43 (2020), no. 8, 5179–5196.
10. Wang Sheng, Hu Guixin, Wei Tengda, Wang Linshan, Permanence of hybrid competitive Lotka-Volterra system with Lévy noise. Physica A: Statistical Mechanics and its Applications, 2020, 540.
11. Guixin Hu, The explicit expression of non-trivial stationary distribution of SDEs under regime switching, Applied Mathematics Letters, 107 (2020) 106479.
12. Zhan-Ping Ma. Spatiotemporal dynamics of a diffusive Leslie-Gower prey-predator model with strong Allee effect. Nonlinear Analysis: Real World Applications, 2019, 50: 651-674

学术交流
近年来,团队成员与国内外同行合作有着密切合作,获得一系列具有国际先进水平的创新成果。通过多次邀请知名专家来校交流、举办线上学术会议等方式加深同行对公司的了解。

(图为2021年举办中国数学会奇异摄动专业委员会学术年会)
(图为2020年举办常微分方程与动力系统研讨会(线上))

(图为2023年团队成员参加奇异摄动专业委员会第十八届学术年会)

(图为2023年团队成员参加第十届全国微分方程定性理论会议)
